How does this sound to you?
There is no universally applicable, objective way to measure the distance between two phonemes1. Intuitively, it seems like some sounds are definitely closer than others—for example, the consonants “t” and “p” sound more similar to a native English speaker than “t” and “s”. But how would you rank whether “t” is closer to “g” or “m”? And how would you go about comparing consonants to vowels?
Motivation
I’m working on a project to identify names with the same pronunciation in order to create name popularlity rankings and visualizations that combine different spelling variations of the same name. As a first step, I prompted a generative AI model to produce phonetic transcriptions of name pronunciations. In order to group names, and recommend similar-sounding names, I needed a way to rank pronunciation similarity. This turned out to be much more difficult than I expected.
Overview
There are two related questions to consider here:
- Which phoneme sounds do you consider most similar, and how do you quantify that similarity or difference?
- How do you align phonetic transcriptions of different lengths? What determines which sounds are considered “dropped” when comparing pronunciations of different lengths?
Measuring phoneme similarity
Broadly, there are three major approaches that have been used to measure similarity between English phonemes, listed in order of decreasing effort and increasing robustness:
- Confusability: in experimental settings, how often are different sounds confused by listeners? Administering a controlled experiment is time-consuming and expensive. Moreover, judgments of sounds in isolation don’t generalize to the real world, so devising an experiment with a sample that’s representative of everyday speech would require impractically long lab sessions.
- Expert judgment: how many phonological features, like place of articulation, manner of articulation, and voicing, are shared between two phonemes? Even understanding what these features are requires a lot of domain-specific knowledge, let alone calibrating a scoring system based on them.
- Substitution: how often is one sound substituted for another in phonetic transcriptions of the same word? Computing substitution frequencies from words with multiple human-annotated pronunciations in open-source pronouncing dictionaries is basically a sequence alignment problem.
- Dictionary creators, however, rarely assign more than one “correct” pronunciation to a given word; the whole point of a pronunciation dictionary is to provide a single, canonical pronunciation for each word. Moreover, experts are often biased towards a “standard” accent that glosses over real-world regional variations in the way people speak.
- To supplement the limited pool of “gold standard” pronunciation variations, I turned to an approach that researchers have called “decoder error.” Decoder error looks at how often a model-based system substitutes one phoneme for another when generating phonetic transcriptions for a given word. Uncertainty in the model’s output reflects uncertainty in the model’s training data, providing an empirical way to measure phoneme interchangeability.
from pathlib import Pathimport polars as plimport numpy as npimport seaborn as snsimport matplotlib.pyplot as plt# apply seaborn plotting themesns.set_theme(style='whitegrid')Phonological Phoneme Similarity
The phoneme similarity features I’m using are based on work by Ruiz et al for a 2014 paper on aligning transcripts to audio in an automatic subtitling system2. I copied the matrix into a CSV, added the missing ZH phoneme, flattened columns, and added back the Rhotic feature from the Kondrak 2002 thesis which Ruiz et al. derived their matrix from.
I’m using the ARPAbet phoneme set, which is designed specifically to cover sounds used in American English. This is the format used by the CMU Pronouncing Dictionary, which is the most comprehensive and widely used source of human-annotated phonetic transcriptions freely availble to the public. ARPAbet has the major advantage representing pronunciations entirely in ASCII (regular letters and numbers), which makes it more accessible and easier to work with than specialist transcription systems like IPA.
ruiz_features = pl.read_csv(Path.cwd().joinpath('ruiz_phoneme_features.csv'))with pl.Config(tbl_rows=ruiz_features.height):display(ruiz_features)| Phoneme | Vowel | Place | Place_Score | Manner | Manner_Score | Voiced | Nasal | High | Back | Round | Long | Rhotic |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| str | i64 | str | i64 | str | i64 | i64 | i64 | i64 | i64 | i64 | i64 | i64 |
| “AA” | 100 | “velar” | 60 | “low vowel” | 0 | 100 | 0 | 0 | 50 | 0 | 100 | 0 |
| “AE” | 100 | “palatal” | 70 | “low vowel” | 0 | 100 | 0 | 0 | 100 | 0 | 0 | 0 |
| “AH” | 100 | “velar” | 60 | “mid vowel” | 20 | 100 | 0 | 50 | 50 | 0 | 0 | 0 |
| “AO” | 100 | “velar” | 60 | “low vowel+high vowel” | 0 | 100 | 0 | 0 | 50 | 100 | 100 | 0 |
| “AW” | 100 | “velar” | 62 | “low vowel+high vowel” | 16 | 100 | 0 | 40 | 30 | 40 | 100 | 0 |
| “AY” | 100 | “palatal” | 70 | “low vowel+high vowel” | 16 | 100 | 0 | 40 | 70 | 0 | 100 | 0 |
| “B” | 0 | “bilabial” | 100 | “stop” | 100 | 100 | 0 | null | null | null | null | null |
| “CH” | 0 | “palato-alveolar” | 75 | “affricate” | 90 | 0 | 0 | null | null | null | null | null |
| “D” | 0 | “alveolar” | 85 | “stop” | 100 | 100 | 0 | null | null | null | null | null |
| “DH” | 0 | “dental” | 90 | “fricative” | 80 | 0 | 0 | null | null | null | null | null |
| “EH” | 100 | “velar” | 60 | “mid vowel” | 20 | 100 | 0 | 50 | 100 | 0 | 0 | 0 |
| “ER” | 100 | “velar” | 70 | “mid vowel” | 20 | 100 | 0 | 50 | 50 | 0 | 100 | 100 |
| “EY” | 100 | “palatal” | 70 | “mid vowel+high vowel” | 28 | 100 | 0 | 70 | 100 | 0 | 100 | 0 |
| “F” | 0 | “labiodental” | 95 | “fricative” | 80 | 0 | 0 | null | null | null | null | null |
| “G” | 0 | “velar” | 60 | “stop” | 100 | 0 | 0 | null | null | null | null | null |
| “HH” | 0 | “glottal” | 10 | “fricative” | 80 | 0 | 0 | null | null | null | null | null |
| “IH” | 100 | “palatal” | 70 | “mid vowel” | 20 | 100 | 0 | 50 | 100 | 0 | 0 | 0 |
| “IY” | 100 | “palatal” | 70 | “high vowel” | 40 | 100 | 0 | 100 | 100 | 0 | 100 | 0 |
| “JH” | 0 | “palato-alveolar” | 75 | “affricate” | 90 | 0 | 0 | null | null | null | null | null |
| “K” | 0 | “velar” | 60 | “stop” | 100 | 0 | 0 | null | null | null | null | null |
| “L” | 0 | “alveolar” | 85 | “approximant” | 60 | 0 | 0 | null | null | null | null | null |
| “M” | 0 | “bilabial” | 100 | “stop” | 100 | 100 | 100 | null | null | null | null | null |
| “N” | 0 | “alveolar” | 85 | “stop” | 100 | 100 | 100 | null | null | null | null | null |
| “NG” | 0 | “velar” | 60 | “stop” | 100 | 100 | 100 | null | null | null | null | null |
| “OW” | 100 | “velar” | 62 | “mid vowel+high vowel” | 28 | 100 | 0 | 70 | 0 | 100 | 100 | 0 |
| “OY” | 100 | “palatal” | 64 | “mid vowel+high vowel” | 28 | 100 | 0 | 70 | 40 | 0 | 0 | 0 |
| “P” | 0 | “bilabial” | 100 | “stop” | 100 | 0 | 0 | null | null | null | null | null |
| “R” | 0 | “alveolar” | 85 | “approximant” | 60 | 100 | 0 | null | null | null | null | null |
| “S” | 0 | “alveolar” | 85 | “fricative” | 80 | 0 | 0 | null | null | null | null | null |
| “SH” | 0 | “palato-alveolar” | 75 | “fricative” | 80 | 0 | 0 | null | null | null | null | null |
| “T” | 0 | “alveolar” | 85 | “stop” | 100 | 0 | 0 | null | null | null | null | null |
| “TH” | 0 | “dental” | 90 | “fricative” | 80 | 0 | 0 | null | null | null | null | null |
| “UH” | 100 | “velar” | 60 | “high vowel” | 40 | 100 | 0 | 100 | 0 | 0 | 0 | 0 |
| “UW” | 100 | “velar” | 60 | “high vowel” | 40 | 100 | 0 | 100 | 0 | 100 | 100 | 0 |
| “V” | 0 | “labiodental” | 95 | “fricative” | 80 | 100 | 0 | null | null | null | null | null |
| “W” | 0 | “velar+bilabial” | 80 | “approximant” | 60 | 0 | 0 | null | null | null | null | null |
| “Y” | 0 | “palatal” | 60 | “approximant” | 60 | 100 | 0 | null | null | null | null | null |
| “Z” | 0 | “alveolar” | 85 | “fricative” | 80 | 0 | 0 | null | null | null | null | null |
| “ZH” | 0 | “palato-alveolar” | 75 | “fricative” | 80 | 100 | 0 | null | null | null | null | null |
Feature-based similarity scoring
Using these phonological features to score similarity between two phonemes requires considering different sets of features when comparing only vowels vs. comparisons that involve a consonant. These features come from a field of study known as Articulatory Phonetics and convey different aspects of how sounds are formed during speech by the human vocal tract. This article from the University of Sheffield’s Center for Linguistics Research provides a concise overview that I found helpful.
Greg Kondrak’s thesis explains why each set of features is relevant for each comparison type. I modified the “salience” weights used for each set of features to scale the scores between [0, 100], to make the numbers friendlier to work with during calibration, although the final similarity scores are all between [0, 1]. I also added a novel penalty term to reflect my intuition that vowels are more likely to be swapped than consonants among different pronunciations of the same term.
Every aspect of feature-based scoring requires some manual calibration; the values I arrived at were derived from the Ruiz paper as well as Kondrak’s thesis, with some additional manual tuning. As with any system incoroporating human judgment, subjectivity is inescapable. My methods here are valid in so far as they yield useful results.
phonemes = ruiz_features['Phoneme'].to_list()
# convert features into a dictionary by phonemeruiz_features_dict = {row['Phoneme']: row for row in ruiz_features.rows(named=True)}
# note: weights don't need to sum to 1; for example, any two vowels have a baseline level of similarity of 20/100.# columns and corresponding weights for scoring similarity between two vowelssalience_weights_v2v = {"High": 0.15,"Back": 0.15,"Round": 0.15,"Long": 0.05,'Rhotic': 0.3}# columns and corresponding weights for scoring similarity between two consonants, or a consonant and a vowelsalience_weights_c2c_c2v = {"Vowel": 0.1, # penalty for comparing a vowel to a consonant or vice versa"Place_Score": 0.375,"Manner_Score": 0.475,"Voiced": 0.1,"Nasal": 0.05,}
# base score is the maximum possible score (self-similarity).# all feature differences are scaled by the salience weights and subtracted from the base score.base_score = 100
def phonetic_feature_based_similarity_score(ph1, ph2):features1 = ruiz_features_dict[ph1]features2 = ruiz_features_dict[ph2]# recall: values other than 0 are True in Pythonif features1['Vowel'] and features2['Vowel']:salience_weights = salience_weights_v2velse:salience_weights = salience_weights_c2c_c2vscore = base_scorefor field, weight in salience_weights.items():score -= weight * abs(features1[field] - features2[field])return score
# test our intuition from earlier: what phonemes are most similar to "T"?test_phoneme = 'T'test_similarities = [(p, phonetic_feature_based_similarity_score(test_phoneme, p)) for p in phonemes]test_similarities = pl.DataFrame(test_similarities, orient='row', schema=['phoneme', f'similarity_to_{test_phoneme}'])\.sort(f'similarity_to_{test_phoneme}', descending=True)plt.figure(figsize=(6, 8))sns.barplot(data=test_similarities, x=f'similarity_to_{test_phoneme}', y='phoneme', orient='y')plt.title(f'feature-based similarity of {test_phoneme} to other ARPAbet phonemes')plt.show()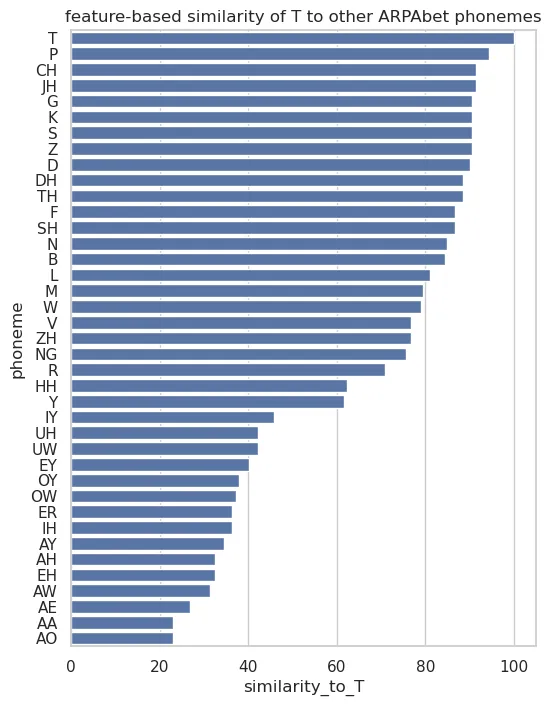
From phonemes to pronunciations
So now we have a way to measure the similarity between two phonemes. But how do we measure the similarity between two pronunciations?
If the pronunciations are the same length, it’s easy: we can just add up the similarity scores for each phoneme pair and divide by the number of phoneme pairs. But what if the pronunciations are different lengths? How do we determine which phoneme pairs “align” and which phonemes represent insertions or deletions?
To resolve this problem we can borrow a technique from bioinformatics: the Needleman-Wunsch algorithm. This algorithm is used to align two sequences of DNA or protein sequences, and works by finding the optimal alignment between two sequences by considering all possible alignments and scoring them based on similarity.
Building a substitution matrix
In order to use the Needleman-Wunsch algorithm to align phoneme sequences, we need to build a substitution matrix from our feature-based similarity scores. We could use Needleman-Wunsch without a substitution matrix by using the same penalty for all substitutions, but when applied to phoneme sequences a constant penalty results in a combinatorial explosion of possible optimal alignments with uninformative similarity scores3.
The off-diagonal entries of this matrix represent the “cost” of substituting one phoneme for another, which is lower (less negative) the more similar the two phonemes are. The diagonal entries represent how much the similarity score improves as a result of matching the same phoneme in both pronunciations. Finally, the “gap penalty” Needleman-Wunsch input determines how much the similarity score degrades as a result of matching a phoneme in one pronunciation with a gap in the other pronunciation (an “insertion” or “deletion”). Empirically some phonemes are more likely to be dropped than others, but we can’t determine this from feature-based similarity scores alone.
While I won’t be implementing or applying Needleman-Wunsch here, we can use the substitution matrix here to visualize the pairwise similarity across all phonemes in a single heatmap chart.
# fill in substitution matrix with feature-based similarity scoressub_mtx = np.zeros((len(phonemes), len(phonemes)))for i, phoneme1 in enumerate(phonemes):for j, phoneme2 in enumerate(phonemes):score = phonetic_feature_based_similarity_score(phoneme1, phoneme2)if phoneme1 != phoneme2:# mismatch scores are <similarity score> - 100,# so that substitutions between more similar pairs incur a smaller penaltyscore -= base_scoresub_mtx[i, j] = score
# divide by base_score to get scores in [0, 1]sub_mtx = sub_mtx / base_score
# heatmapplt.figure(figsize=(10, 8))sns.heatmap(sub_mtx, xticklabels=phonemes, yticklabels=phonemes, cmap='coolwarm', linewidths=0.5, linecolor='black');plt.title('feature-based substitution matrix for ARPAbet phonemes')plt.show()
# housekeeping: save similarity matrix as a numpy array in current directory for use in next notebook.np.save('phoneme_feature_based_substitution_matrix.npy', sub_mtx)
Conclusion & next steps
The feature-based phoneme similarity scores we computed in this article, and visualized in the heatmap above, are most useful as groundwork for aligning pronunciations to count substitutions in the “decoder error”-based approach that I ultimately chose as the most suitable for measuring pronunciation similarity. The best use of feature-based similarity scores is to align different pronunciations of the same word to count substitutions.
In practice, feature-based similarity scores don’t produce interesting similarity rankings for name pronunciations because there are too many ties and because there’s no obvious way to measure how likely a phoneme is to be omitted from a pronunciation. There are too many parwise phoneme comparisons in our substitution matrix (1600 in all including gaps) for linguists to produce properly nuanced similarity rankings based on subject-matter expertise. Moreover, considering phonemes in isolation misses phenomena like the “flap T” or unreleased stop, where “T” can sometimes sound like “D” when it appears between vowels (e.g. “party” sounds like “pardy”).
The rather unsatisfying answer from this investigation is that, even within a single language, theoretical linguistics doesn’t offer an objective way to measure how similar two sounds are, much less how similar two pronunciations are. The theoretical basis for using features from Articulatory Phonetics is that sounds which are produced in a similar way are more likely to be confused by the speaker, which is a shaky foundation when you consider that what we’re really trying to measure is how similar two sounds seem to the listener.
In the next article in this series, I’m going to walk through using the Needleman-Wunsch algorithm to align pronunciations of the same word to count substitutions and calibrate those counts into a matrix we can use to rank the similarity of any two pronunciations.
References
Bailey, Todd M., and Ulrike Hahn. 2005. “Phoneme Similarity and Confusability.” Journal of Memory and Language 52 (3): 339–62. https://doi.org/10.1016/j.jml.2004.12.003.
Kondrak, Grzegorz. 2002. “Algorithms for Language Reconstruction.” https://webdocs.cs.ualberta.ca/~kondrak/papers/thesis.pdf.
Ruiz, Pablo, Aitor Álvarez, and Haritz Arzelus. 2014. “Phoneme Similarity Matrices to Improve Long Audio Alignment for Automatic Subtitling.” International Conference on Language Resources and Evaluation, May, 437–42. http://www.lrec-conf.org/proceedings/lrec2014/pdf/387_Paper.pdf.
“Phoneme Similarity Matrices.” n.d. Accessed January 8, 2025. https://sites.google.com/site/similaritymatrices/.
Footnotes
Ruiz, Pablo, Aitor Álvarez, and Haritz Arzelus. 2014. “Phoneme Similarity Matrices to Improve Long Audio Alignment for Automatic Subtitling.” International Conference on Language Resources and Evaluation, May, 437–42. ↩
Needleman-Wunsch with constant penalties is essentially equivalent to Levenshtein distance, which is a measure of the minimum number of single-character edits (insertions, deletions, or substitutions) required to change one sequence into another. ↩